1. Méthodes de tris
Pour pouvoir étudier des données, il est souvent nécessaire de les trier par ordre croissant ou décroissant.
Il existe différentes méthodes pour cela.
Ces algorithmes diffèrent par leurs complexités et leurs efficacités.
Pour visualiser différents algorithmes de tri :
https://www.toptal.com/developers/sorting-algorithms
Pour réviser et découvrir d’autres algorithmes de tris ;
l’article sur les algorithmes de tris
2. Tri par sélection
Un premier fichier présentant les 3 algorithmes de tris vus en cours :
from random import randint
def liste_aleatoire(n):
# générer aléatoirement un liste de taille n
# contenant des nbres entiers entre 0 et 100
return [randint(0,100) for i in range(n)]
def inverse_liste(a):
# inverse les termes de la liste
retour=[]
for i in range(len(a)):
retour.append(a[len(a)-1-i])
return retour
def triee(a):
# indique si une liste est triée
for i in range(len(a)-1):
if a[i]>a[i+1]:
return False
return True
def tri_selection(a):
# trie une liste par ordre croissant
# par l'algo de tri par selection
for i in range(len(liste)-1):
# pour voir le déroulement de l'algorithme
# print(a)
indice_min=i
for j in range(i,len(liste)):
if a[j]<a[indice_min]:
indice_min=j
a[i],a[indice_min]=a[indice_min],a[i]
return a
def tri_bulles(a):
# trie une liste par ordre croissant
# par l'algo de tri par bulle
liste=a.copy()
for i in range(len(liste)):
# pour voir le déroulement de l'algorithme
#print(liste)
for j in range(len(liste)-1):
if liste[j+1]<liste[j]:
liste[j+1],liste[j]=liste[j],liste[j+1]
# pour voir le déroulement de l'algorithme
#print(liste)
return liste
3. Tri par insertion
def tri_insertion(a):
# trie une liste par ordre croissant
# par l'algo de tri par insertion
for i in range(0,len(liste)-1):
j=i+1
val=a[j]
while j>0 and a[j-1]>val:
a[j]=a[j-1]
j=j-1
a[j]=val
#print(i,j,a)
4. Comparer des méthodes de tris
Un programme permettant de comparer le temps mis par ces différents algorithmes :
import tris
from timeit import timeit
import pylab
#timeit(setup='from tris import tri_select; from listes import cree_liste_melangee',stmt='tri_select(cree_liste_melangee(10))',number=100)
def mesure_temps(tri,longueur):
'''
retourne le temps maximal pour trier par tri par sélection de 100 listes mélangées de longueur 10
: longueur : (int) longueur des listes à trier
: CU :
: return : (list) une liste contenant le temps des listes de longueurs 1,2,......, longueur
'''
liste_temps=[]
for i in range(0,longueur):
temp = timeit(setup='from tris import '+ tri +'; from tris import liste_aleatoire',stmt=tri+'(liste_aleatoire('+str(i)+'))',number=100)
liste_temps.append(temp)
return liste_temps
def affichage(type_tri,longueur):
'''
affiche le graphique représentant les temps maximums pour 100 listes triées de taille donnée
'''
correspondance = {# on crée un dictionnaire de correspondances
"selection":"tri_selection", #
"insertion":"tri_insertion",
"bulles":"tri_bulles",
"sort":"tri_sort",
}
longueur_listes=[i for i in range(1,longueur+1)]
# return correspondance[type_tri]
liste_temps=mesure_temps(correspondance[type_tri],longueur)
NBRE_ESSAIS = 100
pylab.title('Temps du tri '+type_tri+' (pour {:d} essais)'.format(NBRE_ESSAIS))
pylab.xlabel('taille des listes')
pylab.ylabel('temps en secondes')
pylab.grid()
pylab.plot(longueur_listes,liste_temps)
pylab.savefig("graphique "+type_tri+".png")
pylab.show()
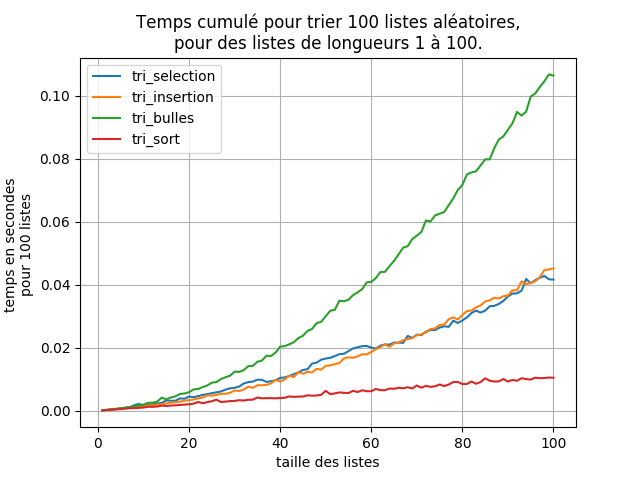
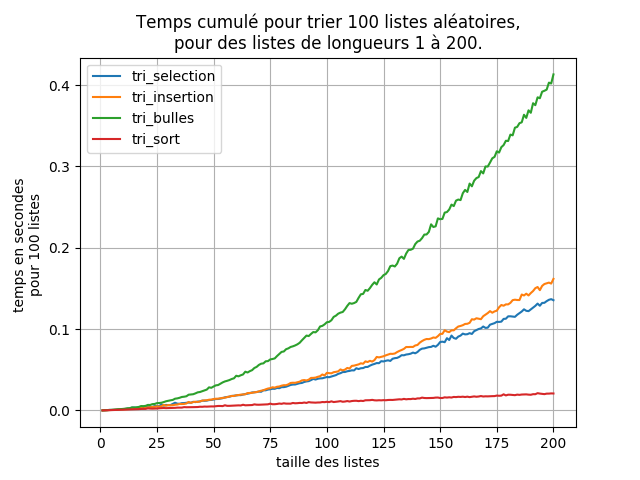
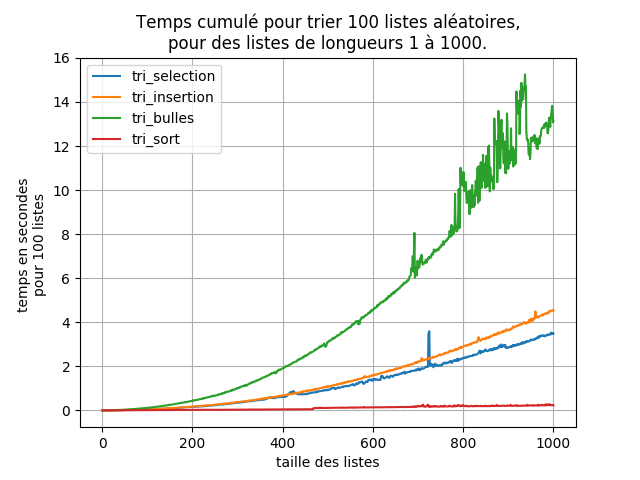
def comparaison_tris(longueur):
longueur_listes=[i for i in range(1,longueur+1)]
# return correspondance[type_tri]
NBRE_ESSAIS = 100
pylab.title('Temps cumulé pour trier {:d} listes aléatoires,'.format(NBRE_ESSAIS)+'\npour des listes de longueurs 1 à '+str(longueur)+'.')
pylab.xlabel('taille des listes')
pylab.ylabel('temps en secondes \npour {:d} listes '.format(NBRE_ESSAIS))
pylab.grid()
pylab.plot(longueur_listes,mesure_temps("tri_selection",longueur),label="tri_selection")
pylab.plot(longueur_listes,mesure_temps("tri_insertion",longueur),label="tri_insertion")
pylab.plot(longueur_listes,mesure_temps("tri_bulles",longueur),label="tri_bulles")
pylab.plot(longueur_listes,mesure_temps("tri_sort",longueur),label="tri_sort")
pylab.legend()
pylab.savefig("graphique comparaisons.png")
pylab.show()
comparaison_tris(1000)