En informatique, un algorithme est un « ensemble de règles opératoires dont l’application permet de résoudre un problème énoncé au moyen d’un nombre fini d’opérations. Un algorithme peut être traduit, grâce à un langage de programmation, en un programme exécutable par un ordinateur. » d’après la définition du Larousse.
Algorithme 1 : Déterminer si un nombre entier est premier.
On peut présenter un algorithme sous la forme d’un schéma :
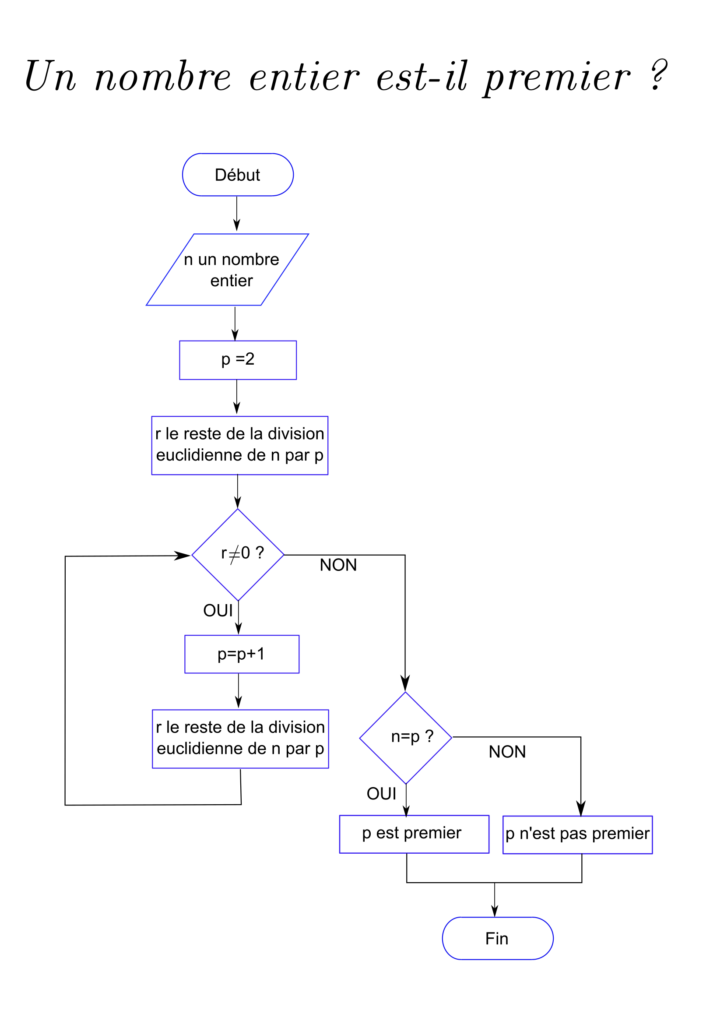
Ou sous la forme d’une phrase :
« Pour savoir si un nombre entier n différent de 1 est premier, on teste tous les diviseurs entiers compris entre 2 et n-1. Si on trouve un diviseur, le nombre n’est pas premier sinon il l’est »
On désire créer un programme Python permettant de déterminer si un nombre est premier.
On peut proposer en première approche :
def est_premier(nombre):
# on traite le cas particulier n=1
if nombre==1:
return False
# on utilise une boucle for permettante
# de faire décrire à i tous les nombres entiers
# de 2 à nombre - 1
for i in range(2,nombre):
# on regarde si le reste de la division
# euclidienne de n par i est égal à 0
if nombre%i==0:
# n a un diviseur, on renvoie False
return False
# on n'a pas trouvé de diviseurs, on renvoie True
return True
Application 1:
Un nombre de Fermat est un nombre qui peut s’écrire sous la forme 22n + 1, avec n entier naturel. Le n-ième nombre de Fermat, 22n + 1, est noté Fn.
Ces nombres doivent leur nom à Pierre de Fermat, qui émit la conjecture que tous ces nombres étaient premiers.
Les nombres F5, F6 et F7 sont-ils premiers ?
Peut-on améliorer son programme pour le rendre plus rapide ?
Exercice 1
On considère un nénuphar spécial de 10 cm2 sur le lac d’Annecy. Il double de surface tous les mois. Déterminer combien d’années il lui faudra pour recouvrir la surface totale du lac. On utilisera un programme en Python permettant de répondre à la question.